L'interferenza: descrivere le basi fisiche del fenomeno e dare un esempio in cui gioca un ruolo essenziale.
L'interferenza è un effetto tipico della propagazione per onde, che si manifesta quando due moti oscillatori di eguale frequenza e differenza di fase costante interessano la stessa regione spaziotemporale. Fra i primi ad occuparsi di questo fenomeno fu Thomas Young, che dimostrò con esso la natura ondulatoria della luce, confutando la teoria corpuscolare di Newton. L'apparato sperimentale di Young era costituito da una sorgente luminosa puntiforme e monocromatica, illuminante uno schermo con due piccoli fori: per il principio di Huygens, i fori si comportavano come sorgenti secondarie di onde luminose sferiche coerenti, e in fase per costruzione, cosicché la luce da essi prodotta produceva interferenza: si osservavano a valle dei fori delle zone di massimo illuminamento e delle zone oscure, corrispondenti alle superfici iperboliche ventrali e nodali.
Alla base della comprensione teorica del fenomeno vi è la semplice legge per la composizione delle ampiezze dei moti oscillatori: le ampiezze prodotte da ciascun foro al punto P, distante r
1 dal primo foro e r2 dal secondo, sono scrivibili come
x
1 = x01 sin (wt - kr1)x
2 = x02 sin (wt - kr2)
e la differenza di fase in P è
d = k (r1 - r2)
per cui, con la tecnica dei vettori rotanti, si trova l'ampiezza risultante in P come
x P = ( x012+x022 + 2x01x02cos d )1/2,
e il termine cosinusoidale produce gli effetti costruttivi e distruttivi tipici dell'interferenza. Ad esempio, se le ampiezze
x01 e x02 sono eguali, per l'intensità di illuminamento si trova l'espressione
I
P = 4x02 cos2 d/2.
Quello descritto è un effetto del tutto generale, che si applica senza particolari modifiche a qualsiasi moto ondulatorio, e in particolare anche alla propagazione degli oggetti quantistici: in effetti, una delle più classiche dimostrazioni del comportamento ondulatorio della materia è fornita dallo stesso esperimento di Young applicato a fasci di elettroni o neutroni termici. A causa di ciò, gli esempi di interferenza abbondano tanto nella fisica classica quanto nella fisica moderna; i più classici nel secondo caso sono forse l'interferenza distruttiva che sta alla base del principio di esclusione per i fermioni, e i più recentemente studiati effetti di interferenza elettrodebole nei processi mediati dallo scambio di fotoni o di bosoni Z. Nel breve spazio a mia disposizione vorrei però trattare gli effetti di interferenza che si osservano in un sistema fisico davvero notevole per la sua semplicità e grande bellezza: quello dei mesoni K neutri.
Le particelle K
0 sono la componente inferiore di un doppietto di isospin di mesoni di stranezza +1, (K+, K0). Sono prodotte in gran quantità per interazione forte: un buon esempio ne sono le reazioni utilizzate fin dagli anni '50 per ottenerle in produzione associata con iperoni nello scattering di pioni su protoni:
p- p ® K0 S0, (1)
® K0 L0;
l'antiparticella del K
0, di stranezza -1, può invece essere prodotta da pioni solamente in processi a tre o più corpi: 00 sdsds
00000
0
0000
d
p- p ® K0bar L0bar n n (2)
p+ p ® K+ K0bar p
ed ha quindi una soglia energetica di produzione più elevata.
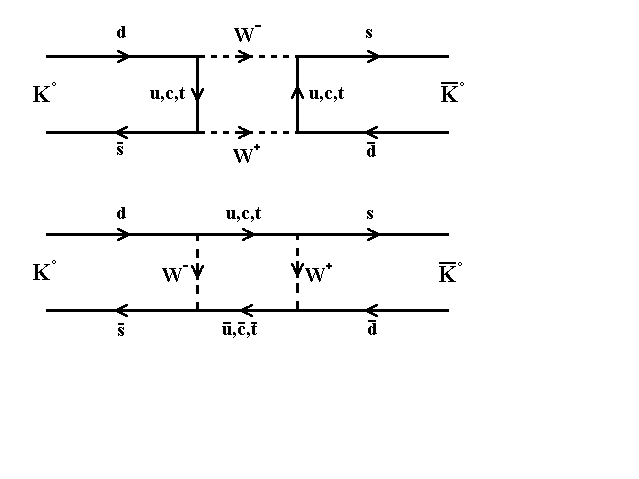
Gli stati |K0> e |K0bar> sono autostati di stranezza. S è un buon numero quantico per le interazioni forti, che conservano l'ipercarica Y = (B+S)/2, (B è il numero barionico), ma non lo è per le interazioni deboli, a causa del mixing nella matrice di Cabibbo-Kobajashi-Maskawa. In effetti, queste particelle decadono per interazione debole perché non esistono stati a stranezza non nulla più leggeri. Sono poi possibili anche transizioni con variazioni di due unità di S, al second'ordine della costante GF: esse possono dar luogo alle transizioni |K0> Û |K0bar> per mezzo dei grafici schematizzati nella figura seguente.

Un altro numero quantico di importanza rilevante nei decadimenti dei mesoni K è quello associato all'operazione composta CP, prodotto della coniugazione di carica C e dell'inversione spaziale P: poiché C scambia tra loro particella e antiparticella, l'operazione associata CP scambia tra loro i due stati. Se ipotizziamo che le interazioni deboli, responsabili del decadimento dei mesoni K neutri, siano invarianti per CP (cosa che è vera solo in prima approssimazione, ma non inficia la discussione che segue nei suoi risultati essenziali), saranno gli autostati di questo operatore a distinguersi nei decadimenti, per cui ci torna utile costruire le seguenti combinazioni lineari:
|K01> = 2-1/2 ( |K0> + |K0bar> ) ( CP +1 )
|K02> = 2-1/2 ( |K0> - |K0bar> ) ( CP -1 ).
Il decadimento principale della combinazione a CP positiva è in due pioni carichi (circa 2/3 delle volte) o neutri (1/3), mentre lo stato a CP negativa non può andare in due pioni, e i suoi decadimenti non leptonici danno luogo a tre pioni neutri oppure uno stato p+p-p0. Data la notevole differenza nello spazio delle fasi di questi decadimenti, le vite medie dei due stati sono molto diverse: t1 = 0.9 10-10, t2 = 0.5 10-7.
A causa delle oscillazioni descritte poc'anzi, fra i K1 e i K2 vi è anche una piccola differenza di massa: lo si vede sviluppando i valori di aspettazione dell'hamiltoniano debole su questi stati, supponendo di porci nel loro sistema a riposo:
m1 = <K1| H |K1> =
= 1/2 [ <K0| H |K0> + <K0bar| H |K0bar> +
+ <K0| H |K0bar> + <K0bar| H |K0> ]
m
2 = <K2| H |K2> == 1/2 [
<K0| H |K0> + <K0bar| H |K0bar> +- <K0| H |K0bar> - <K0bar| H |K0> ]
da cui
Dm12 = <K0| H |K0bar> + <K0bar| H |K0> .
Questa differenza di massa gioca il ruolo di una differenza di fase fra le ampiezze dei K
1 e K2, e rende osservabili i fenomeni di interferenza fra i due stati. Se si parte da un fascio di |K0> puri a t = 0, si osservano dapprima i decadimenti in due pioni della componente K1 a vita media breve, e molto più a valle i decadimenti in tre pioni della componente K2, di CP negativa. Ma la curva dell'intensità di decadimenti in coppie di pioni non è una semplice esponenziale, ma un'esponenziale con un termine oscillatorio sovrapposto. Lo si capisce scrivendo esplicitamente la dipendenza temporale degli stati K1 e K2, e inserendola in quella dei K0: da
|K
1(t)> = a1 (t) |K1> = exp (im1t) exp (G1t/2) |K1>|K
2(t)> = a2 (t) |K2> = exp (im2t) exp (G2t/2) |K2>
si ottiene
| K
0 (t) > = 2-1/2 [ |K1(t)> + |K2(t)> ] == 1
/2 [ (a1(t)+a2(t)) |K0> + (a1(t)-a2(t)) |K0bar> ]
e quindi, per l'intensità della componente K
0 all'istante t,
I
K0(t) = 1/4 IK0(0) {exp(-G1t)+exp(-G2t)+2exp[-(G1+G2)t/2] cos(Dm t)}.
Questo effetto di interferenza quantistica è a mio avviso di grande bellezza. Se gli stati avessero vita media infinita, a causa del fenomeno oscillatorio vi sarebbe una totale conversione da uno stato all'altro ogni
p/Dm secondi!La misura della quantità
Dm/m che si può ricavare sperimentalmente per i mesoni K1 e K2 dalla misura della frequenza di decadimenti in due pioni è una delle più precise in assoluto della fisica moderna, dato che
D
m = 3.5 10-12 MeV,
e
Dm/m è misurabile con un errore relativo di 10-17.