p+ + p ® p+ + p (1)

p- + p ® p0 + n (2)

p- + p ® p- + p (3)

scoprirono nella curva della sezione d'urto dei processi (1) e (3) in funzione dell'energia dei pioni incidenti la prima metà di quella che studi successivi confermarono essere la curva di risonanza di una nuova particella. Questo stato, denominato D(1232), e più tardi riconosciuto in quattro stati di carica, è la prima risonanza scoperta in fisica delle particelle elementari. Ad essa seguì la scoperta di una messe di altri stati adronici a vita media di molti ordini di grandezza inferiore alle particelle elementari fino ad allora note (p,n,p,K,m,e), che a poco a poco permise di rivelare una soggiacente struttura spettroscopica.

La risonanza D(1232), come tutte quelle che le seguirono, è caratterizzata da una classica forma della sezione d'urto del processo (1) che dà luogo alla sua formazione: questa si ricava dall'analisi dello scattering con onde sferiche parziali di momento angolare definito; si trova, per l'ampiezza di scattering elastico, l'espressione

f(q) = 1/k Sl (2l + 1) (e2idl - 1)/2i Pl(cosq),

ove dl indica lo spostamento di fase dell'onda parziale l-esima, e Pl sono i polinomi di Legendre. f(q) ha valore massimo quando la fase dl attraversa il valore p/2: in corrispondenza a tale valore, si può scrivere

F(l) = (e2idl - 1)/2i = 1/(cotg dl - i),

cotg d(E) = cotg d(Er) + (Er-E) [- d cotg d(E)/dE]E=Er + ...

ove Er è l'energia alla quale si ha risonanza; in tale condizione d vale p/2, per cui si può trascurare cotg d(Er) e ponendo

[- d cotg d(E)/dE]E=Er = 2/G

F(l) = G/2 * [ (Er-E) - iG/2]-1,

sel = 4p/k2 Sl (2l + 1) gs G2/4 * [ (Er-E)2 - G2/4 ],

formula nota come curva di risonanza di Breit-Wigner. Il fattore gs tiene conto delle molteplicità di stati di spin degli stati iniziale e finale, ed è pari a

gs = (2J+1) / (2sp+1)(2s_b+1),

se J è il momento angolare dello stato formato in risonanza e sp,sb sono gli spin di proiettile e bersaglio.

A partire dal 1952 furono scoperti, in esperimenti di formazione come quello ora visto, o in produzione associata con altri corpi, molti nuovi stati risonanti adronici. L'analisi della sezione d'urto per questi processi permise di assegnare a ciascuna risonanza un ben definito numero barionico B, ipercarica Y, carica elettrica Q; e lo studio del comportamento di s in funzione dell'angolo di emissione, ovvero della sezione d'urto differenziale ds/dW, permise l'assegnazione dei numero quantici di spin e parità; fu dunque proposto da Geoffrey Chew un principio di "democrazia nucleare", secondo cui questi stati risonanti dovessero essere considerati del tutto equivalenti alle particelle che decadevano per interazione debole, sebbene queste ultime mostrassero vite medie di almeno 10 ordini di grandezza superiori. La vita media degli stati risonanti era infatti deducibile dalle larghezze G delle curve di risonanza. Si ottenevano per G misure dell'ordine della decina o del centinaio di MeV/c2, e si potevano quindi calcolare da t=h/2pG per gli stati risonanti vite medie dell'ordine dei 10-24 secondi, sintomo di un'alta intensità per la forza responsabile del decadimento (e anche della loro produzione, dato l'alto valore della sezione d'urto).

Ben presto, nella gran quantità di stati prodotti, si cominciò ad intravedere uno schema: la spettroscopia adronica si rivelò del tutto simile a quella atomica, con stati eccitati di energia superiore che decadevano negli stati fondamentali. 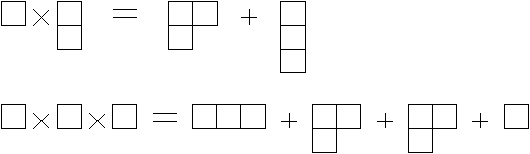Nel 1964 Murray Gell-Mann propose una organizzazione degli stati scoperti in multipletti del gruppo di simmetria SU(3) attraverso l'ipotesi che ciascuna risonanza fosse in realtà uno stato composto da due o tre corpi elementari, detti quarks, rappresentazioni irriducibili del gruppo di simmetria, a spin 1/2, carica elettrica frazionaria (+2/3 o -1/3) e numero barionico 1/3. Il gruppo SU(3) era l'unico candidato in grado di fornire multipletti della molteplicità giusta: come si vede dalle decomposizioni in diagrammi di Young

per i barioni è possibile ipotizzare una composizione di tre quarks, che fornisce gli osservati ottetti di nucleoni e il decupletto delle risonanze D,S*,X e W, e per i mesoni funziona bene il modello di una coppia quark-antiquark, che dà l'ottetto dei pioni e dei K. Le previsioni di Gell-Mann (e Nishijima) sulla struttura statica degli adroni rimasero un modello interessante ma non confermato fino al 1974, quando la comunità scientifica internazionale dovette convincersi dell'esistenza dei quarks dall'evidenza prodotta da due diversi esperimenti.

In quell'anno a Brookhaven Samuel Ting conduceva un esperimento in cui protoni da 30 GeV venivano diretti su un bersaglio in berillio, e due spettrometri magnetici misuravano (con l'aiuto di contatori Cerenkov e di tempo di volo) l'impulso di coppie di elettroni prodotte nelle collisioni: si trattava di un affinamento di un precedente esperimento di Leon Lederman, che aveva analizzato invece le coppie di muoni prodotte in collisioni simili, con una risoluzione energetica inferiore a causa dello scattering coulombiano multiplo che questi subivano nell'attraversare la materia inserita per discriminare i muoni da altri corpi. Ting ottenne una curva di risonanza in corrispondenza a 3.1 GeV/c2 di massa invariante della coppia elettrone-positrone, segnale della creazione di uno stato di massa superiore a tutte le altre particelle fino ad allora note; a tale stato il gruppo di Brookhaven diede temporaneamente il nome J.

R = s (e+e- ® adroni) / s (e+e- ® m+m-),

che fornisce informazioni sul numero di quarks di cui la materia è composta, dato che il fotone virtuale in cui la coppia elettrone-positrone annichila può materializzarsi (con probabilità proporzionale al quadrato della carica elettrica) in ciascuna delle coppie particella-antiparticella energeticamente permesse: con tre quarks ci si aspetta per R il valore 3*(4/9+1/9+1/9), ove 3 è un fattore dovuto al colore dei quarks, mentre con un quarto quark a carica +2/3 il rapporto deve salire di altri 4/3. Per misurare R veniva aumentata in steps di 100 MeV l'energia del centro di massa, ma quando la sezione d'urto a 3.1 GeV si mostrò anormalmente alta venne scandagliata la zona in intervalli più piccoli, e venne così scoperta la risonanza y, anormalmente stretta, e di massa 3097 MeV/c2. La larghezza risultava irrisolvibile con la strumentazione disponibile, dato che la risoluzione sull'energia del c.m. era limitata (a un paio di MeV) dalle incertezze sulla misura dell'energia dei proiettili.

Nel novembre del 1974 entrambi i gruppi vennero a conoscenza dei risultati dell'altro esperimento, e pubblicarono insieme la scoperta della particella, che da allora è nota come J/y. La risonanza J/y convinse ben presto i fisici dell'esistenza dei quarks, per tre motivi. In primo luogo, essa era stata prevista quattro anni prima da Glashow, Iliopoulos e Maiani sulla base di uno studio della non osservazione di decadimenti in due muoni dei mesoni K0; in secondo luogo, la sua vita media "lunga" (di tre ordini di grandezza superiore a quella delle normali risonanze adroniche) riceveva perfetta spiegazione dalla cromodinamica quantistica, come mostrarono Appelqvist e Politzer in un loro lavoro del 1975, in cui, ipotizzando l'esistenza di stati legati cc, spiegarono con precisione la larghezza dei suoi decadimenti in adroni; e infine, la scoperta di altri stati di caratteristiche simili (la y(3770) e gli stati c0,c1,c2) mostrò ben presto come vi fosse una somiglianza praticamente perfetta con gli stati eccitati del positronio e+e-: la J/y era sicuramente uno stato legato di una coppia quark-antiquark, e doveva trattarsi di uno stato di tripletto, in onda S e con numeri quantici JPC=1--.

Glashow ed i suoi collaboratori avevano studiato il processo K0 ®m+m-X, che è permesso in un modello a tre quarks per scambio di corrente debole neutra, e dovrebbe avere una probabilità simile al corrispondente processo a corrente carica, K+®m+nX, che è uno dei principali canali di decadimento del kaone positivo. Ma sperimentalmente si osservava una differenza di molti ordini di grandezza fra le probabilità dei due decadimenti. Se vi sono tre quarks, e si descrive il mescolamento della componente inferiore del doppietto (u,d') con l'angolo di Cabibbo q, l'ampiezza dei decadimenti è proporzionale al quadrato del fattore

J = (u, d cosq+s sinq) t3 (u, d cosq + s sinq) =

uu - dd cos2q - ss sin2q - (ds + sd) sinq cosq,

e quindi correnti neutre che tramutano un quark s in un quark d sono possibili, con il risultato che il decadimento in due muoni del K0 dovrebbe essere ben visibile. GIM proposero l'esistenza di un quarto quark c, che formava un secondo doppietto assieme alla combinazione ortogonale dei quarks d e s: (c, -d sinq + s cosq). In questo modo, all'espressione ora vista per J va aggiunto il fattore

(c,-d sinq + s cosq) t3 (c,-d sinq + s cosq) =

cc - dd sin2q - ss cos2q + (ds + sd) sinq cosq,

con una conseguente cancellazione dei termini che permettono transizioni s-d. Un decadimento in due muoni dei K0 poteva invece avvenire, secondo GIM, mediante diagrammi a scatola come quelli in fig.3, ovviamente con frequenza molto inferiore a causa della piccolezza della costante di accoppiamento debole. In più, gli elementi di matrice relativi ai due diagrammi in cui viene scambiato un quark u o un quark c hanno segni opposti, causando una cancellazione che non è esatta solo a causa della diseguaglianza delle masse quadrate dei quarks u e c. Da questo fatto, e dai dati sperimentali sul decadimento, Glashow Iliopoulos e Maiani erano giunti alla conclusione che il quark c doveva avere massa compresa fra 1 e 3 GeV/c2, in completo accordo con la massa ricavabile da quella della J/y.

Appelqvist e Politzer avevano studiato le possibilità di decadimento di uno stato cc, di massa inferiore alla soglia di produzione di due mesoni D (stati legati cd o cu), e dedotto che il decadimento in adroni doveva avvenire, come per la particella f (stato legato ss), mediante lo scambio tra stato iniziale e finale, di tre gluoni: lo scambio di un solo gluone non è possibile, poiché lo stato cc è singoletto di colore; e la transizione cc ® gg viola la coniugazione di carica, dato che J/y ha gli stessi numeri quantici del gluone. La larghezza della J/y nel suo decadimento adronico dipende allora dal fattore as6/M2, che è di due ordini di grandezza inferiore per la J/y che per la f, a causa della diminuzione da 0.4 a 0.22 della "costante" as fra l'energia dei due decadimenti.

Ancora più stupore suscitò la regolarità con la quale la massa degli stati risonanti al di sopra della J/y imitava la spettroscopia del positronio. Il lavoro conclusivo sulla spettroscopia degli stati cc fu compiuto dall'esperimento Crystal Ball, che riuscì ad identificare anche gli stati di singoletto 1S, denominati hc. La regolarità con cui i vari stati cc imitano la spettroscopia del positronio è dovuta all'alta massa del quark c, che permette una trattazione non relativistica del potenziale di legame.