Non equilibrium statistical mechanics is a good candidate to understand biological systems and their emergent behaviors. Typically such systems are kept away from equilibrium with a continuous input of energy. At present there is not an understanding such as the one reached in the equilibrium statistical mechanics. Furthermore a fundamental approach like the maximum entropy principle for the equilibrium counterpart is still lacking. The emergence of critical like behavior and universality in far from equilibrium systems is very fascinating but still in its in childhood.

Universal scaling behavior is an attractive feature in statistical physics because a wide range of models can be classified purely in terms of their collective behavior whose characteristics depend only on few details like the dimensionality of the system and symmetries of the problem (eventually on the kind of decay of the interaction strength) but not on finer details. Scaling phenomena, as epitomized by fine size scaling, have been observed in many branches of physics,chemistry, biology, ecology economics and sociology. Our research interests include ecological and biological systems, physics of interacting particle, optimal transportation network, complex networks dynamics with applications on environmental science and sustainability.

Understanding the origin, maintenance and loss of biodiversity in ecological systems is a goal of the highest scientific priority given the rapidity of global biodiversity loss. Ecological communities exhibit pervasive patterns and interrelationships between size, abundance, and the availability of resources. Non-equilibrium statistical mechanics is the natural candidate to develop a unified framework for understanding the distribution of organism sizes, their energy use, and spatial distribution. We have demonstrated that optimal use of resources, both at the individual and community level, leads to a consistent scaling theory in plant communities which is well supported by observational data. We believe that variational/optimization principles, which have been so successful in physics, are also able to explain other commonly observed spatio-temporal patterns in natural systems (e.g. architecture of ecological interaction networks, species area relationship) and, eventually, predict new ones not yet discovered. Our research of complex living systems incorporates theoretical inquiry, modeling, and empirical study.
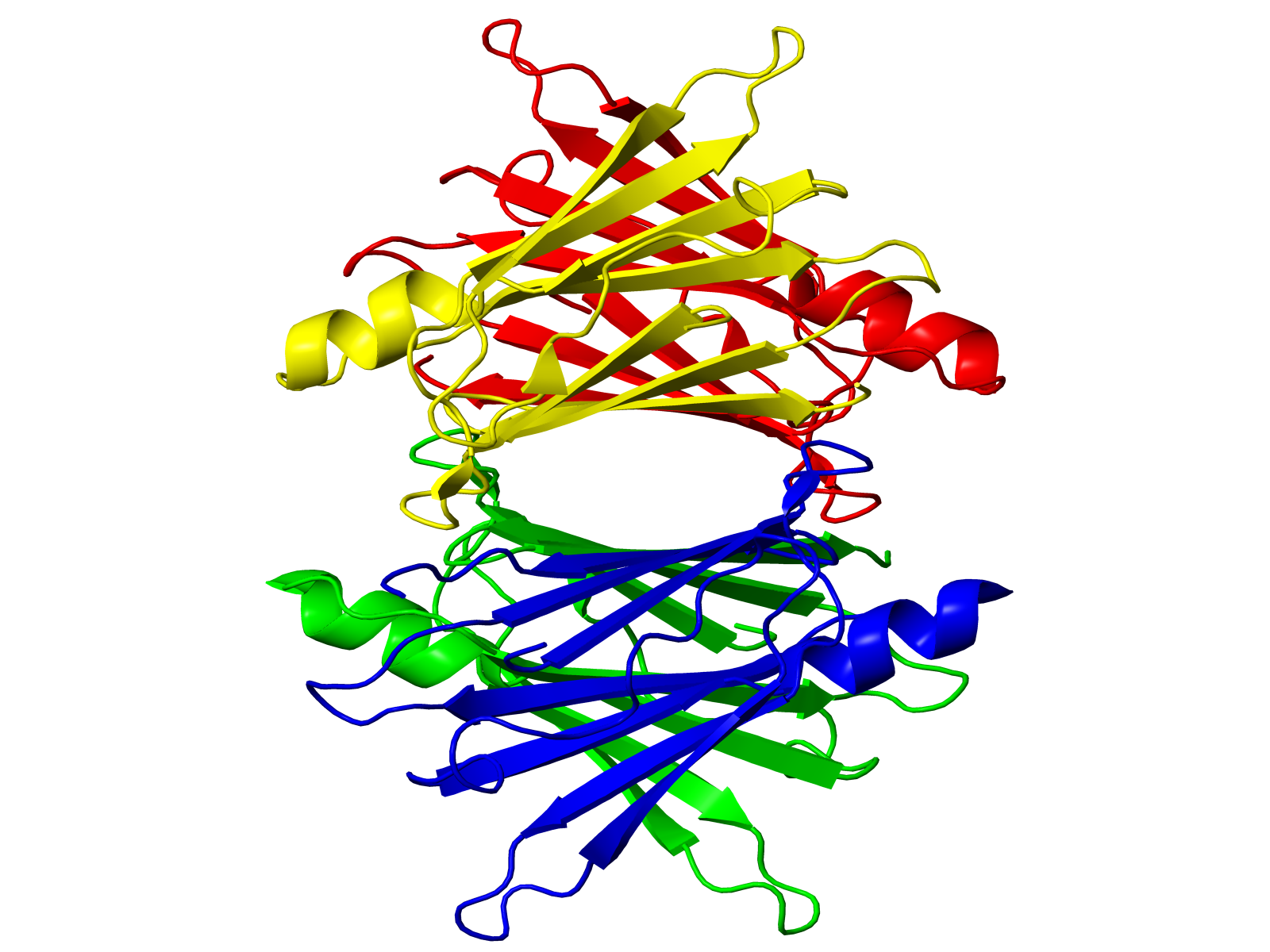
Globular proteins are a key component of the network of life. The protein problem is one of formidable complexity. The number of degrees of freedom of the protein atoms as well as the surrounding water molecules, which play an essential role in the folding process, is enormous. Physics has provided an understanding of the essential features underlying the phases of inanimate matter in terms of the principles of geometry and symmetry. A similar simple understanding of the physics of proteins has been lacking. Our work points to a unification of the various aspects of all proteins: symmetry and geometry determine the limited menu of folded conformations that a protein can choose from for its native state structure; these structures are in a marginally compact phase in the vicinity of a phase transition and are therefore eminently suited for biological function; these structures are the molecular target for the powerful forces of evolution; proteins are well-designed sequences of amino acids which fit well into one of these predetermined folds; and proteins are prone to misfolding and aggregation leading to the formation of amyloids, which are implicated in debilitating human diseases such as Alzheimer's, light-chain amyloidosis and spongiform encephalopathies. The experimental data and the new approach reveal an astonishing simplicity underlying the protein problem. Based on the lesson learnt from biopolymers we have presented a framework for the predictive design of nano-machines. Even in the absence of sequence heterogeneity, protein-like behavior is obtainable for a simple chain molecule with "context" dependent interactions